
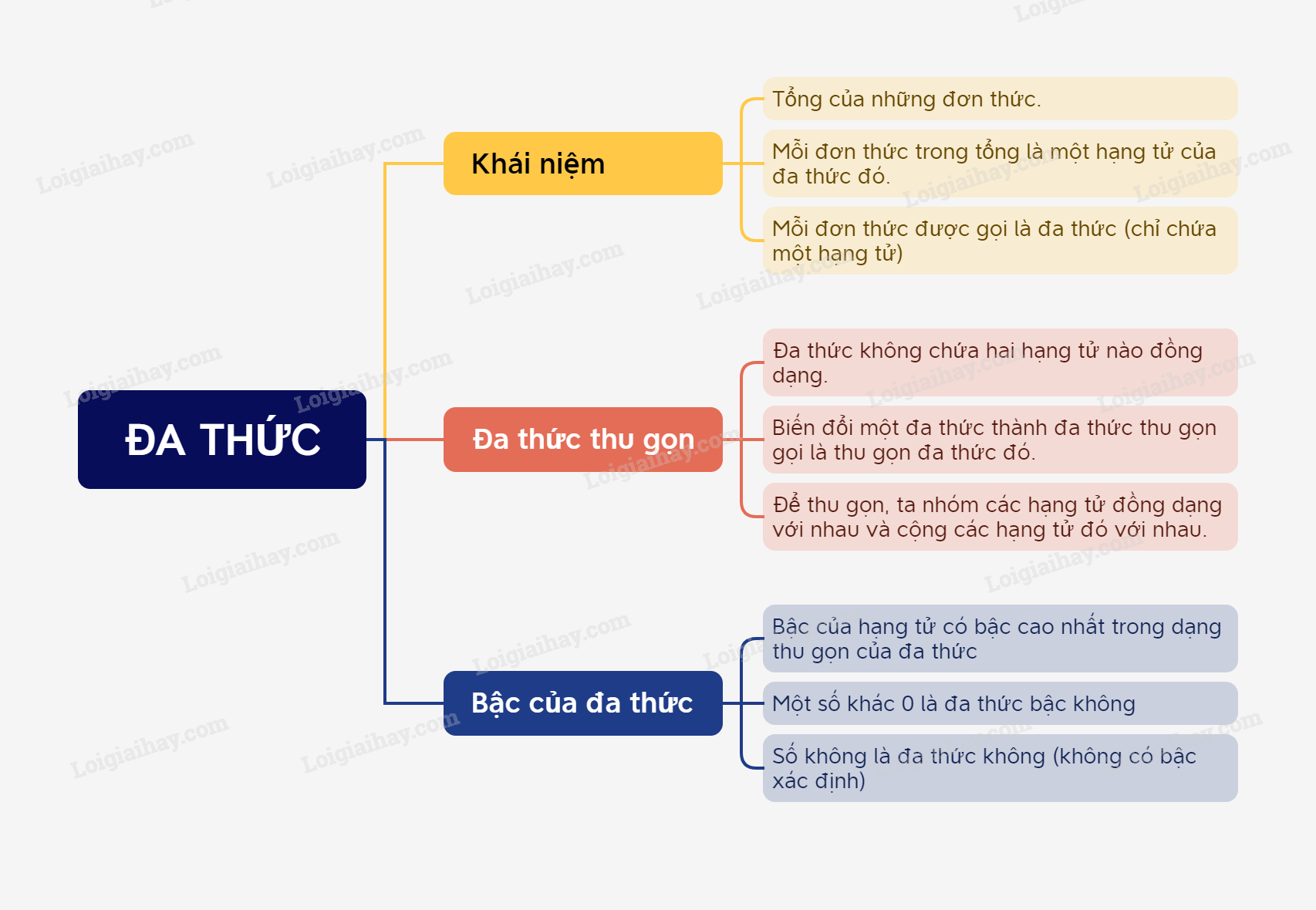
Đa thức là một tổng của những đơn thức.
Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).
Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.
Ví dụ:
\[ x^2-4x+3;x^2+3xyz^2-yz+1;(x+3y)+(2x-y) \] là đa thức
\[ \frac{(x+3y)}{(2x-y)};\frac{(x^2+2)}{(x^2-y^2)} \] không phải là đa thức
\[ x^2-4x+3 \] có 3 hạng tử
\[ x^2;-4x;3 \]
\[ x^2+3xyz^2-yz+1 \] có 3 hạng tử
\[ x^2;3xyz^2;-yz;1 \]
Đa thức thu gọn là đa thức không chứa hai hạng tử nào đồng dạng.
Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.
Đa thức thu gọn
là đa thức không chứa hai hạng tử nào đồng dạng.
Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.
Ví dụ:
\[ A=x^3-2x^2y-x^2y+3xy^2+y^2 \]
\[=x^3-3x^2y+3xy^2+y^2 \]
Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.
Một số khác 0 tùy ý được coi là một đa thức bậc 0.
Số 0 cũng là một đa thức, gọi là đa thức không. Nó không có bậc xác định.





kuvip789 is growing on me! Found some really cool niche games I haven’t seen anywhere else. The bonuses are alright too. Give’em a peek: kuvip789
Okay, so I tried out taigamvipg88 the other day. Honestly, had a decent time! The interface is pretty slick, and there’s a good selection of games. Nothing groundbreaking, but definitely worth checking out if you’re looking for something new. Give taigamvipg88 a spin!
Fabet Snowsell, ok, sounds interesting and unique, is it trustworthy? See for yourself: fabetsnowsell